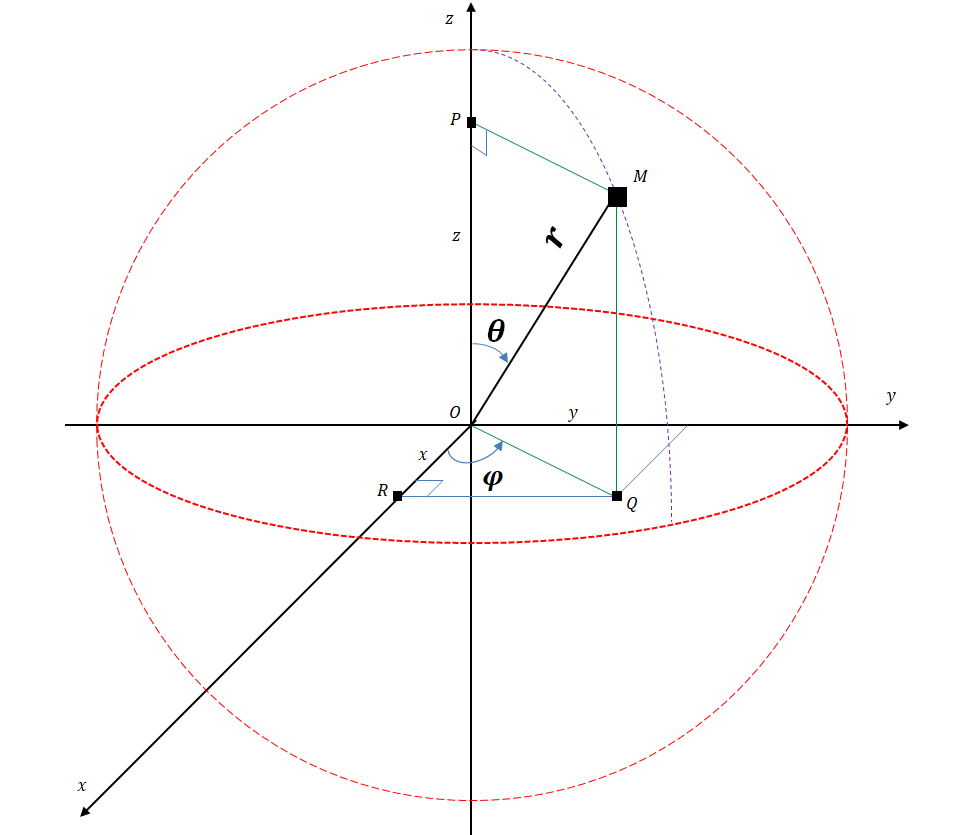
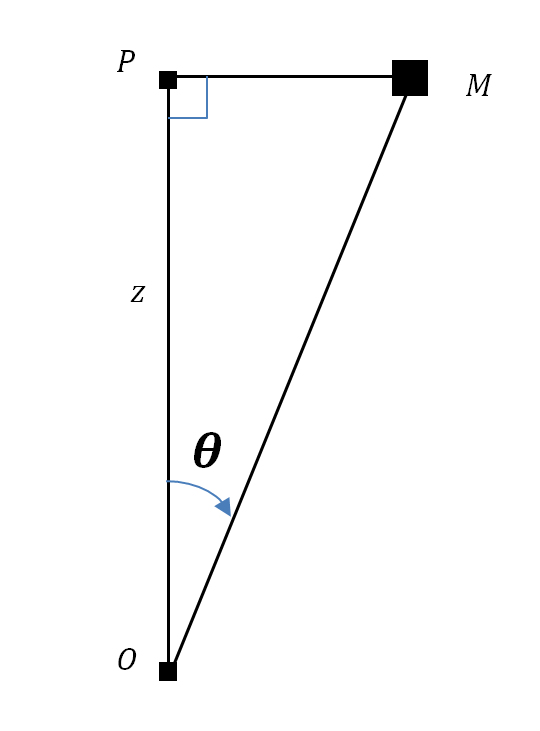
On considère le triangle \( (OMP) \) qui est rectangle en \(P\) :		$$ cos \theta = \frac{OP}{OM} = \frac{z}{r} $$ $$ z = r \ cos \theta $$ $$ PM = OQ = r \ sin \theta $$
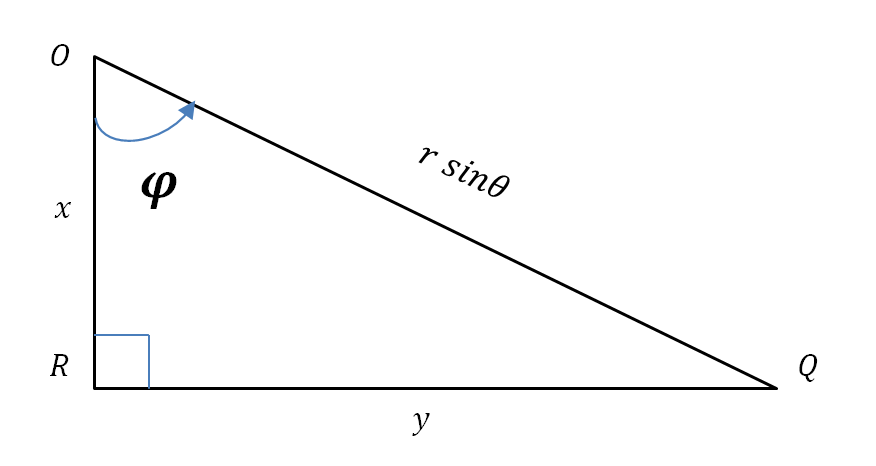
On considère maintenant le triangle \( (ORQ) \) rectangle en \(R\)		$$ x = OR = OQ \ cos \varphi = r \ sin \theta \ cos \varphi $$ $$ y = RQ = OQ \ sin \varphi = r \ sin \theta \ sin \varphi $$

-->